Quantum Computing vs Classical Cryptography: A Deep Dive
Category: Cryptography
Unlocking the Future: Quantum Computing vs Classical Cryptography
As a cybersecurity professional, cryptography enthusiast, or student delving into the intricate world of secret communications, you've undoubtedly encountered the rising buzz around quantum computing and its impact on classical cryptography. Your challenge is understanding how these vastly different computational paradigms affect the security of data, especially as quantum machines promise to break traditional cryptographic schemes. You've likely searched for clear, concise comparisons that distill the core differences, mathematical principles, vulnerabilities, and defenses without drowning in overly technical jargon or speculative claims.
This post is crafted specifically for your level—whether you're sharpening your expertise or expanding your foundational knowledge. We’ll explore the mathematical underpinnings of classical and quantum cryptography, timeline their historical evolution, dissect their operational mechanics, and unravel the looming influence of quantum advancements on the security landscape. Unlike other articles that skim the surface or overwhelm with math-heavy rhetoric, this blog offers a balanced, well-structured exploration rooted in current research and practical insights. Read on to equip yourself with sharp, actionable understanding that prepares you for the quantum era of cryptography.
- Unlocking the Future: Quantum Computing vs Classical Cryptography
- Foundations of Classical Cryptography
- Introduction to Quantum Computing
- Overview of Quantum Cryptography
- Quantum Algorithms Threatening Classical Cryptography
- Vulnerabilities of Classical Cryptographic Schemes in the Quantum Era
- Post-Quantum Cryptography: Exploring Quantum-Resistant Algorithms and Deployment Challenges
- Comparative Analysis: Strengths and Weaknesses of Classical vs Quantum Cryptography
- Historical Perspective: Evolution of Cryptography Leading Up to the Quantum Age
- Impact of Quantum Technology on Secret Communications: The Future Landscape
- Mathematical Challenges and Open Problems in Quantum vs Classical Cryptography: Research Frontiers and What Lies Ahead
Foundations of Classical Cryptography
Classical cryptography rests on robust mathematical principles that ensure secure communication by transforming readable information (plaintext) into an obscured format (ciphertext) only decipherable by intended recipients. At the heart of these systems lie hard mathematical problems, such as integer factorization and discrete logarithms, which underpin the security assumptions of many encryption algorithms. By leveraging these principles, classical cryptography provides confidentiality, integrity, authentication, and non-repudiation in digital communications.
Core Mathematical Principles
- Number theory: Concepts like prime numbers and modular arithmetic form the basis for asymmetric cryptosystems.
- Algebraic structures: Groups, rings, and elliptic curves are pivotal in constructing efficient and secure algorithms.
- Computational hardness assumptions: The difficulty of solving problems such as factoring large composite numbers or computing discrete logarithms ensures that breaking encryption remains computationally infeasible with classical resources.
Common Algorithms and Their Security Assumptions
-
RSA (Rivest-Shamir-Adleman)
RSA's security hinges on the integer factorization problem—factoring a large number into its prime components is computationally prohibitive for classical computers. This asymmetric cryptosystem enables secure key exchange and digital signatures but requires sufficiently large key sizes (2048 bits or more) to withstand attacks. -
AES (Advanced Encryption Standard)
AES is a widely adopted symmetric-key cipher based on the substitution-permutation network paradigm. It relies on block cipher transformations and key-dependent substitutions. Unlike RSA and ECC, AES security depends on the infeasibility of brute-force key search within a key space typically of 128, 192, or 256 bits, combined with resistance to cryptanalysis techniques. -
ECC (Elliptic Curve Cryptography)
ECC utilizes the algebraic structure of elliptic curves over finite fields, offering comparable security to RSA but with significantly smaller key sizes. Its security rests on the Elliptic Curve Discrete Logarithm Problem (ECDLP), considered hard to solve with classical algorithms, enabling efficient encryption, key exchange, and digital signatures.
Together, these algorithms form the backbone of existing secure communication systems worldwide. Their security assumptions, rooted in classical computational difficulty, have been the gold standard for decades. However, as quantum computing advances, the very hardness that protects RSA and ECC faces unprecedented challenges, while symmetric algorithms like AES remain more resilient, albeit requiring longer keys. Understanding these foundations is crucial to grasp how quantum computing threatens and reshapes modern cryptography.

Image courtesy of Markus Winkler
Introduction to Quantum Computing
Quantum computing represents a revolutionary leap beyond classical computation by harnessing the unique principles of quantum mechanics. Unlike classical bits that are strictly 0 or 1, quantum bits, or qubits, can exist simultaneously in multiple states through a phenomenon called superposition. This intrinsic parallelism allows quantum computers to process a vast number of possibilities at once, offering the potential to solve problems that are intractable for classical machines.
In addition to superposition, entanglement is another cornerstone of quantum computation. Entangled qubits share a correlation so profound that the state of one instantly influences the other, regardless of the distance separating them. This non-classical connection enables quantum algorithms to perform complex operations more efficiently than classical counterparts.
At the operational level, quantum computations are executed through quantum gates, which manipulate qubits similarly to how logic gates function in classical circuits but with the capability to create and control superposition and entanglement. Gates such as the Hadamard, CNOT, and Pauli-X are fundamental to building quantum algorithms that can challenge classical cryptographic assumptions.
Understanding these quantum principles—qubits, superposition, entanglement, and quantum gates—is essential for comprehending how quantum computers threaten the security foundations of traditional cryptography. They underpin groundbreaking algorithms like Shor’s and Grover’s, which respectively target the hardness of factorization and brute-force key search, putting classical asymmetric systems and symmetric encryption at unprecedented risk. Exploring these concepts equips us to anticipate the cryptographic upheaval ushered in by quantum technology and to innovate defenses resilient to its power.
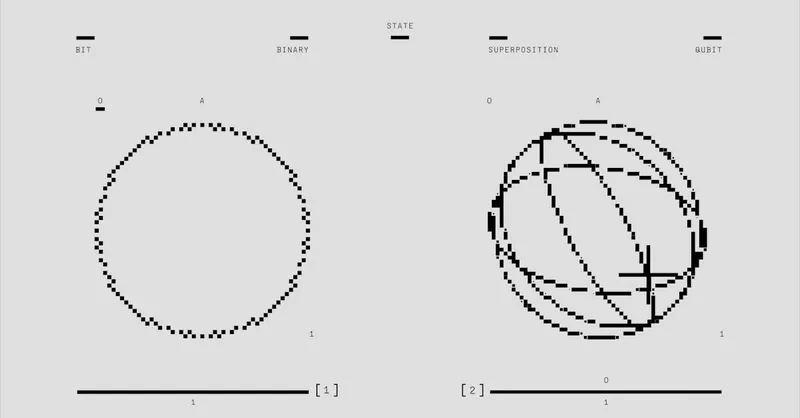
Image courtesy of Google DeepMind
Overview of Quantum Cryptography
Quantum cryptography leverages the fundamental principles of quantum mechanics to create cryptographic protocols that offer security guaranteed by the laws of physics, rather than computational difficulty alone. The most prominent example is Quantum Key Distribution (QKD), a revolutionary method for securely exchanging encryption keys by exploiting quantum phenomena such as superposition and quantum entanglement.
Principles of Quantum Key Distribution (QKD)
QKD protocols enable two parties to generate a shared secret key with the assurance that any eavesdropping attempt will be detected in real time. This is possible because measurement of a quantum system inherently disturbs its state, revealing the presence of an interceptor. Key aspects of QKD include:
- Encoding information in quantum states – Typically, photons' polarization or phase encodes binary information (bits). Due to superposition, these quantum states exist in multiple conditions until measured.
- No-cloning theorem – Unlike classical data, quantum information cannot be copied perfectly. This prevents an adversary from cloning qubits to intercept and resend without detection.
- Detection of eavesdropping – Since any measurement alters the quantum state, QKD protocols include steps to monitor error rates that, above a certain threshold, indicate a security breach.
- Classical post-processing – After quantum transmission, classical communication methods are used for error correction and privacy amplification, ensuring a secure, identical final key.
How Quantum Mechanics Enables Novel Cryptographic Protocols
Unlike classical cryptography that relies on hard mathematical problems (which might be undermined by quantum algorithms), quantum cryptography builds on the immutable rules of quantum physics to create information-theoretic security. This fundamentally changes the game by:
- Eliminating reliance on computational assumptions vulnerable to quantum attacks.
- Providing provably secure key exchange regardless of the eavesdropper’s computing power.
- Enabling advanced protocols like device-independent QKD, which further reduce trust assumptions about hardware.
Quantum cryptography thus offers a paradigm shift—a move from complexity-based security to physics-based security. As quantum technologies mature, QKD and other quantum cryptographic protocols are poised to become critical components in safeguarding communications in the quantum era. Understanding these principles is essential to appreciate how quantum cryptography complements or even supersedes classical schemes under the looming influence of quantum computing advancements.

Image courtesy of Markus Winkler
Quantum Algorithms Threatening Classical Cryptography
Quantum computing’s promise of immense parallelism and novel computational techniques has led to the development of specialized algorithms that can dramatically weaken or even break classical cryptographic schemes. Among these, Shor’s algorithm and Grover’s algorithm stand out as the most critical threats, targeting the core mathematical problems underpinning widely used public-key and symmetric cryptography respectively.
Shor’s Algorithm: Breaking Integer Factorization and Discrete Logarithms
Developed by Peter Shor in 1994, Shor’s algorithm provides an efficient quantum method to factor large integers and compute discrete logarithms exponentially faster than the best known classical algorithms. This directly undermines the security assumptions of foundational asymmetric cryptosystems, including:
- RSA: Relies on the integer factorization problem — Shor’s algorithm can factor large RSA moduli efficiently, allowing an attacker with a sufficiently powerful quantum computer to recover private keys in polynomial time.
- Elliptic Curve Cryptography (ECC): Depends on the hardness of the elliptic curve discrete logarithm problem; Shor’s algorithm can solve this in polynomial time as well, exposing ECC keys to quantum breaches.
- Diffie-Hellman key exchange: Also based on discrete logarithms, which become vulnerable to fast quantum attacks under Shor’s algorithm.
The practical implication is profound: once scalable quantum computers become available, classical asymmetric encryption and digital signatures that safeguard secure internet communications, financial transactions, and data storage could be rendered insecure almost overnight. This has accelerated efforts to develop post-quantum cryptography (PQC) schemes resistant to quantum attacks.
Grover’s Algorithm: Quadratically Accelerating Symmetric Key Search
While asymmetric schemes face existential threats from Shor’s algorithm, symmetric cryptography like AES is comparatively more resilient but not invulnerable. Grover’s algorithm, proposed by Lov Grover in 1996, offers a quantum approach to searching unsorted databases with a quadratic speedup. Applied to cryptography, this translates to:
- Reducing the effective key length of symmetric ciphers, such as AES-256, from 256 bits to approximately 128 bits against brute-force attacks.
- Doubling the vulnerability of symmetric-key algorithms to exhaustive key search, although this is substantially less dramatic than the exponential impact of Shor’s algorithm on asymmetric methods.
To counter Grover’s algorithm, cryptographic recommendations suggest doubling symmetric key sizes to maintain equivalent security margins against plausible quantum attacks. For example, transitioning from AES-128 to AES-256 or even larger keys ensures continued robustness.
Together, Shor’s and Grover’s algorithms reveal critical vulnerabilities in the classical cryptographic landscape by leveraging unique quantum capabilities. Understanding these algorithms not only highlights the urgency for quantum-resistant cryptographic solutions but also underscores the fundamental paradigm shift necessitated by the quantum computing revolution. Keeping abreast of these developments is essential for professionals and enthusiasts aiming to safeguard digital security now and into the quantum future.

Image courtesy of Markus Winkler
Vulnerabilities of Classical Cryptographic Schemes in the Quantum Era
The advent of quantum computing exposes critical vulnerabilities in classical cryptographic schemes, threatening the security foundations that have protected digital communications for decades. Classical asymmetric algorithms like RSA, ECC, and Diffie-Hellman rely on the computational infeasibility of factoring large numbers or solving discrete logarithms—assumptions that quantum algorithms like Shor’s algorithm decisively undermine. Once sufficiently powerful quantum computers become operational, these widely deployed methods face the risk of instantaneous key recovery, rendering encrypted data and digital signatures exposed to adversaries.
Symmetric cryptography, including standards like AES, while more resilient, is not immune. Quantum attacks leveraging Grover’s algorithm could accelerate brute-force key searches, effectively halving the key strength. For instance, AES-128’s security margin diminishes to roughly the equivalent of a 64-bit key against quantum adversaries, which is considered vulnerable by current standards. This necessitates the adoption of larger key sizes—AES-256 and beyond—to maintain robust quantum-era security.
Additional challenges arise from cryptographic protocols and infrastructures built entirely around classical assumptions. Many existing systems lack quantum resistance in areas such as:
- Key exchange mechanisms, which depend on discrete logarithm problems vulnerable to quantum attacks.
- Digital signatures, critical for verifying authenticity but at risk due to efficient quantum factoring.
- Public key infrastructures (PKI) that underpin secure communications but now require quantum-secure alternatives.
The ongoing transition toward post-quantum cryptography (PQC) reflects an urgent response: developing algorithms resistant to quantum attacks without relying on fragile classical hardness assumptions. Until these standards are universally adopted, organizations using classical cryptography must reevaluate risk, prioritize key upgrades, and prepare for a hybrid cryptographic landscape where both classical and quantum-resistant methods coexist to mitigate vulnerabilities exposed by emerging quantum technologies.

Image courtesy of Antoni Shkraba Studio
Post-Quantum Cryptography: Exploring Quantum-Resistant Algorithms and Deployment Challenges
As the quantum threat to classical cryptographic schemes intensifies, post-quantum cryptography (PQC) emerges as the crucial frontier for securing digital communications against both classical and future quantum adversaries. PQC encompasses a collection of quantum-resistant algorithms specifically designed to withstand attacks from quantum computers, ensuring long-term data confidentiality and integrity without relying on the hardness assumptions vulnerable to Shor's and Grover's algorithms. These new cryptographic constructions leverage alternative mathematical problems believed to be intractable for quantum algorithms, such as lattice-based, code-based, multivariate polynomial, and hash-based cryptography.
Leading Quantum-Resistant Algorithm Families
-
Lattice-based cryptography
Built on the hardness of problems like the Learning With Errors (LWE) and Shortest Vector Problem (SVP), lattice-based schemes offer promising efficiency and versatility, suitable for encryption, digital signatures, and key exchange. Examples include CRYSTALS-KYBER and CRYSTALS-DILITHIUM, two finalists in the NIST post-quantum standardization process. -
Code-based cryptography
Utilizing error-correcting codes, schemes such as the McEliece cryptosystem rely on the difficulty of decoding random linear codes. These provide robust security guarantees and fast encryption/decryption speeds but often come with large key sizes. -
Multivariate polynomial cryptography
Based on the hardness of solving systems of multivariate quadratic equations over finite fields, these algorithms are well-suited for digital signatures but generally present larger signature sizes. -
Hash-based signatures
Offering inherently quantum-resistant security by leveraging cryptographic hash functions, schemes like XMSS (eXtended Merkle Signature Scheme) provide practical, provably secure signature methods with minimal assumptions.
Standards Initiatives and Practical Deployment
The National Institute of Standards and Technology (NIST) has spearheaded a rigorous multi-year evaluation to select and standardize PQC algorithms, aiming to facilitate global adoption for securing government, commercial, and critical infrastructure systems. The ongoing process focuses on:
- Assessing security, efficiency, and implementability of candidate algorithms against classical and quantum attack models.
- Balancing key sizes, computational requirements, and communication overhead to fit diverse applications from IoT devices to cloud services.
- Encouraging hybrid models that combine classical and post-quantum algorithms during transition periods to maintain backward compatibility and minimize disruption.
Deploying PQC in real-world environments faces several practical challenges, including:
- Algorithm performance trade-offs, as many quantum-resistant schemes require larger keys or more processing power compared to classical counterparts.
- Integration complexity, needing updates in protocols, hardware, and software stacks, from TLS and VPNs to embedded systems.
- Long-term security validation, ensuring that newly adopted PQC algorithms remain resilient against emerging cryptanalysis and unforeseen quantum advances.
Despite these challenges, proactively adopting post-quantum cryptography is essential to future-proof sensitive communications and data protection. Staying informed about evolving standards, conducting security assessments, and investing in PQC-compatible infrastructure will position organizations to navigate the quantum transition securely and confidently.

Image courtesy of Markus Winkler
Comparative Analysis: Strengths and Weaknesses of Classical vs Quantum Cryptography
As the quantum era advances, understanding the strengths and weaknesses of classical and quantum cryptographic solutions becomes crucial for designing secure, scalable, and practical communication systems. Both paradigms offer unique advantages and face distinct challenges concerning security guarantees, scalability, and implementation complexity.
Security
-
Classical Cryptography
Classical cryptographic schemes rely on computational hardness assumptions such as factoring large integers or solving discrete logarithms. While these provide proven security against classical adversaries, they are fundamentally vulnerable to quantum algorithms like Shor's, which can break popular asymmetric algorithms (e.g., RSA, ECC). Symmetric schemes such as AES are more resilient, yet quantum attacks (Grover’s algorithm) reduce their effective security by roughly half, mandating longer keys for future-proofing. -
Quantum Cryptography
Quantum cryptography, particularly Quantum Key Distribution (QKD), offers information-theoretic security based on the laws of quantum mechanics rather than computational assumptions. This means security is unconditional and immune to advances in computational power, classical or quantum. However, it is mostly limited to key distribution and does not directly provide encryption or digital signatures, necessitating hybrid use with classical symmetric algorithms.
Scalability
-
Classical Cryptography
Classical cryptographic algorithms benefit from established infrastructure, broad compatibility, and mature implementations that scale efficiently from small devices to large networks and cloud systems. They require only classical hardware and support widespread internet protocols. However, their scalability is jeopardized as quantum computers advance, forcing costly key upgrades or migrations to post-quantum algorithms. -
Quantum Cryptography
Quantum cryptographic protocols face significant scalability challenges due to current technological limitations in generating, transmitting, and detecting quantum states over long distances. QKD systems require specialized hardware like single-photon sources and detectors, and the infrastructure for quantum channels (e.g., fiber optics with low loss or quantum repeaters) is still in development. Consequently, quantum cryptography is presently feasible mainly for niche applications or small-scale setups rather than global network deployment.
Implementation
-
Classical Cryptography
Implementation of classical cryptography is straightforward using existing hardware and software ecosystems. Hardware acceleration, optimized libraries, and well-understood standards simplify deployment. Nonetheless, evolving threats from quantum computing necessitate proactive migration to post-quantum cryptography algorithms, which can introduce performance overhead and compatibility concerns during transition periods. -
Quantum Cryptography
Quantum cryptographic implementations require advanced quantum hardware and precise control over quantum phenomena, which are technically complex and expensive. Integration into existing communication frameworks demands additional classical post-processing and hybrid cryptographic approaches. Furthermore, device imperfections and side-channel attacks pose real-world risks, making practical quantum cryptography implementation a sophisticated engineering challenge.
Balancing these factors reveals that while classical cryptography currently remains the backbone of secure communication due to its maturity and scalability, its security foundation is under imminent quantum threat. Conversely, quantum cryptography provides revolutionary, physics-based security but is constrained by implementation hurdles and scalability concerns. The future of secure communication likely involves a hybrid approach, combining post-quantum classical algorithms with quantum cryptographic protocols to harness the strengths of both worlds effectively.

Image courtesy of Markus Winkler
Historical Perspective: Evolution of Cryptography Leading Up to the Quantum Age
Cryptography has always been a dynamic discipline, evolving in response to advances in technology and the ever-changing landscape of communication needs. From early manual ciphers, like the Caesar cipher used in Roman times, to the sophisticated Enigma machine of World War II, each technological leap demanded increasingly complex cryptographic methods to thwart adversaries. The mid-20th century witnessed the birth of modern classical cryptography, grounded in rigorous mathematical theory and computational complexity, exemplified by the development of public-key cryptography in the 1970s. Algorithms like RSA and Diffie-Hellman key exchange revolutionized secure communication by enabling encrypted traffic over open channels without prior shared secrets.
As computing power increased exponentially, so did both the capabilities and threats facing classical cryptography. The rise of the internet and digital communication exponentially expanded the attack surface, pressing cryptographers to enhance algorithmic robustness and scalability. However, this classical trajectory encountered a profound inflection point with the emergence of quantum computing concepts in the 1980s and 1990s. Quantum theory-inspired algorithms, notably Shor’s algorithm, exposed fundamental vulnerabilities in the hardest mathematical problems protecting classical schemes. This revelation reignited cryptographic research, pivoting towards post-quantum cryptography and quantum cryptographic protocols designed for a future where quantum computers reshape the security paradigm.
In summary, the evolution of cryptography is a story of continuous adaptation: from simple substitution ciphers reacting to manual codebreaking, through mathematically grounded algorithms responding to classical computational threats, culminating now in the preparation for the imminent quantum era. Understanding this historical progression is crucial to appreciating why quantum technology challenges the core assumptions of classical cryptography and why the field is vigorously innovating to safeguard the next generation of secure communications.

Image courtesy of Markus Winkler
Impact of Quantum Technology on Secret Communications: The Future Landscape
The integration of quantum technology into secret communications is rapidly transforming the cybersecurity ecosystem, heralding a new era where classical cryptographic methods must coexist and evolve alongside quantum-resistant solutions. This shift demands innovative approaches that blend the strengths of both classical and quantum cryptography to establish secure channels capable of withstanding emerging quantum threats.
Hybrid Cryptographic Models: Bridging Classical and Quantum Security
One of the most promising strategies to safeguard communications in the quantum era involves deploying hybrid cryptographic models. These models combine classical post-quantum cryptographic algorithms with quantum cryptographic protocols like Quantum Key Distribution (QKD) to create layered defenses. Hybrid systems offer several key benefits:
- Enhanced security assurance by leveraging physics-based security from quantum protocols alongside mathematically proven post-quantum algorithms.
- Smooth transition paths that maintain compatibility with existing infrastructure while progressively integrating quantum-resistant mechanisms.
- Mitigation of single-point failures, where the compromise of one system component does not jeopardize the entire communication channel.
This blended approach enables organizations to protect sensitive information with immediate effect and build resilience against future quantum adversaries, making hybrid cryptography a cornerstone of next-generation secure communications.
Secure Quantum Channels and Infrastructure Development
The deployment of secure quantum channels is essential for realizing the full potential of quantum cryptography. Cutting-edge research and technological advancements focus on:
- Quantum networks with low-loss optical fibers and quantum repeaters to extend communication distances without compromising qubit integrity.
- Integration of quantum satellites to facilitate global QKD coverage, overcoming terrestrial limitations.
- Development of quantum-safe communication protocols that incorporate error correction and privacy amplification tailored for real-world noisy quantum environments.
As these infrastructures mature, they promise to enable unconditionally secure communication channels, fundamentally altering how sensitive data is transmitted and protected across sectors like finance, defense, and critical national infrastructure.
Government Policies and Regulatory Frameworks Shaping Quantum Cryptography Adoption
Recognizing the profound implications of quantum technology on cybersecurity, governments worldwide are enacting policies and strategic frameworks to guide the transition toward quantum-safe communications:
- Standardization efforts led by organizations such as NIST and ETSI focus on establishing clear guidelines for quantum-resistant cryptographic algorithms and implementation best practices.
- Funding and incentives support research in quantum cryptography, post-quantum cryptography, and quantum hardware development.
- Regulatory mandates increasingly require critical industries to evaluate quantum risks, conduct cryptographic agility assessments, and plan for post-quantum migration.
- International collaboration aims to align policy and security standards across borders, fostering interoperable and robust quantum communication ecosystems.
These government-led initiatives accelerate the adoption of secure quantum technologies, ensuring that national security, privacy, and economic interests remain protected in the unfolding quantum future.
As quantum computing advances, the future landscape of secret communications will be defined by these hybrid security solutions, expansive quantum infrastructures, and proactive government policies. Embracing this integrated approach is imperative to fortify digital trust and preserve confidentiality in an era shaped by the quantum revolution.

Image courtesy of cottonbro studio
Mathematical Challenges and Open Problems in Quantum vs Classical Cryptography: Research Frontiers and What Lies Ahead
As the clash between quantum computing and classical cryptography intensifies, a set of profound mathematical challenges and open problems emerges at the forefront of cryptographic research. These unresolved issues are pivotal in shaping the future landscape of secure communication, influencing the design of quantum-resistant algorithms, the robustness of quantum cryptographic protocols, and the transition strategies for global cybersecurity infrastructure.
Core Mathematical Challenges in Post-Quantum Cryptography
While promising candidate algorithms for post-quantum cryptography (PQC) have been identified, their foundational hardness assumptions still demand rigorous validation against both classical and quantum adversaries. Key mathematical uncertainties include:
-
Lattice Problem Hardness
The security of lattice-based cryptosystems rests on problems like the Learning With Errors (LWE) and Shortest Vector Problem (SVP). However, fully characterizing the average-case hardness and resistance to novel quantum algorithms remains an active area of investigation. The search for more efficient reductions and tighter security proofs continues to be a critical challenge. -
Code- and Multivariate-based Problems
The decoding problems underlying code-based cryptography, and solving nonlinear multivariate polynomial systems, present rich but not fully explored mathematical terrain. Researchers seek to better understand their structural properties and identify potential quantum algorithmic weaknesses that could emerge with future advances. -
Security Proofs and Parameter Selection
Designing post-quantum schemes with provable security guarantees requires precise parameter tuning to balance security, efficiency, and implementation practicality. This demands deeper mathematical modeling of attack vectors, including side-channel and fault injection attacks, within quantum threat frameworks.
Open Problems in Quantum Cryptographic Protocols
Quantum cryptography offers guarantees grounded in physics, yet it faces fundamental mathematical and engineering questions impacting its long-term viability:
-
Device-Independent Security Models: Developing fully device-independent QKD protocols that eliminate trust assumptions about quantum hardware remains an open problem. Achieving this demands resolving complex issues in quantum nonlocality and entanglement verification with practical resource constraints.
-
Quantum Error Correction and Noise Modeling: Practical deployment requires handling noisy quantum channels and imperfect detectors. Mathematical advancements in quantum error correction codes and realistic noise models are essential to extend secure communication distances and reduce error rates.
-
Composable Security Frameworks: Formulating rigorous, composable security definitions that integrate quantum and classical components seamlessly is a key research frontier. Such frameworks ensure that combining different cryptographic primitives preserves overall system security against adaptive quantum adversaries.
Looking Ahead: Interdisciplinary Research and Quantum-Resistant Innovation
Addressing these mathematical challenges demands interdisciplinary collaboration among cryptographers, quantum physicists, computer scientists, and mathematicians. Fundamental research continues to investigate:
- Novel quantum algorithms that might threaten existing post-quantum candidates, urging the exploration of new hardness assumptions.
- Optimization of quantum-resistant schemes to achieve practical speeds and minimal resource overhead while maintaining robust security.
- Expansion of quantum cryptographic primitives beyond key distribution, including protocols for authentication, secure multi-party computation, and digital signatures within quantum frameworks.
Understanding and resolving these open problems is crucial for developing next-generation cryptographic systems that are not only secure against future quantum attacks but also optimized for real-world implementation. The mathematical frontiers of quantum and classical cryptography thus represent the critical battleground where the future of secure digital communication will be determined.

Image courtesy of Markus Winkler
